Publications

2025

1. 

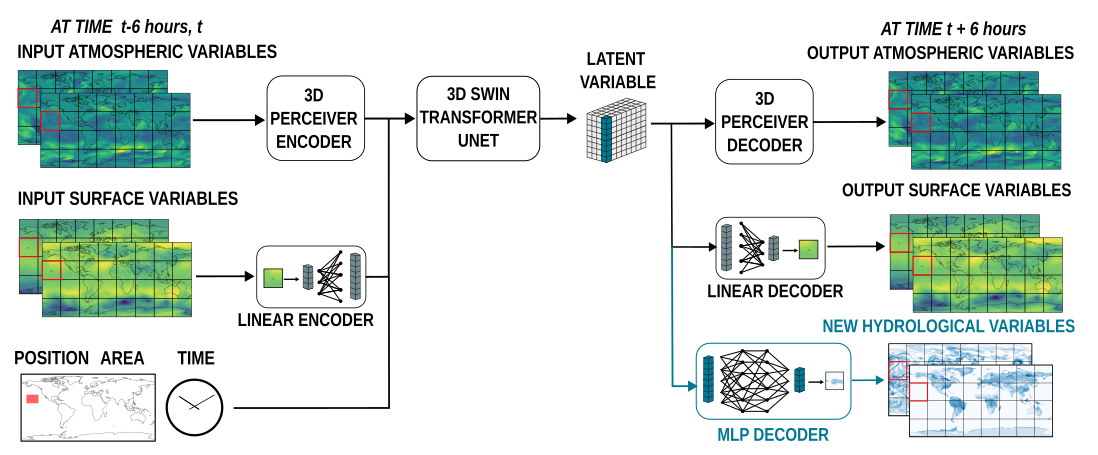   Finetuning a Weather Foundation Model with Lightweight Decoders for Unseen Physical Processes

   Fanny Lehmann, Firat Ozdemir, Benedikt Soja, Torsten Hoefler, Siddhartha Mishra, and Sebastian Schemm

   Jun 2025

   Abs DOI

   Recent advances in AI weather forecasting have led to the emergence of so-called "foundation models", typically defined by expensive pretraining and minimal fine-tuning for downstream tasks. However, in the natural sciences, a desirable foundation model should also encode meaningful statistical relationships between the underlying physical variables. This study evaluates the performance of the state-of-the-art Aurora foundation model in predicting hydrological variables, which were not considered during pretraining. We introduce a lightweight approach using shallow decoders trained on the latent representations of the pretrained model to predict these new variables. As a baseline, we compare this to fine-tuning the full model, which allows further optimization of the latent space while incorporating new variables into both inputs and outputs. The decoder-based approach requires 50% less training time and 35% less memory, while achieving strong accuracy across various hydrological variables and preserving desirable properties of the foundation model, such as autoregressive stability. Notably, decoder accuracy depends on the physical correlation between the new variables and those used during pretraining, indicating that Aurora’s latent space captures meaningful physical relationships. In this sense, we argue that an important quality metric for foundation models in Earth sciences is their ability to be extended to new variables without a full fine-tuning. This provides a new perspective for making foundation models more accessible to communities with limited computational resources, while supporting broader adoption in Earth sciences.

2. 

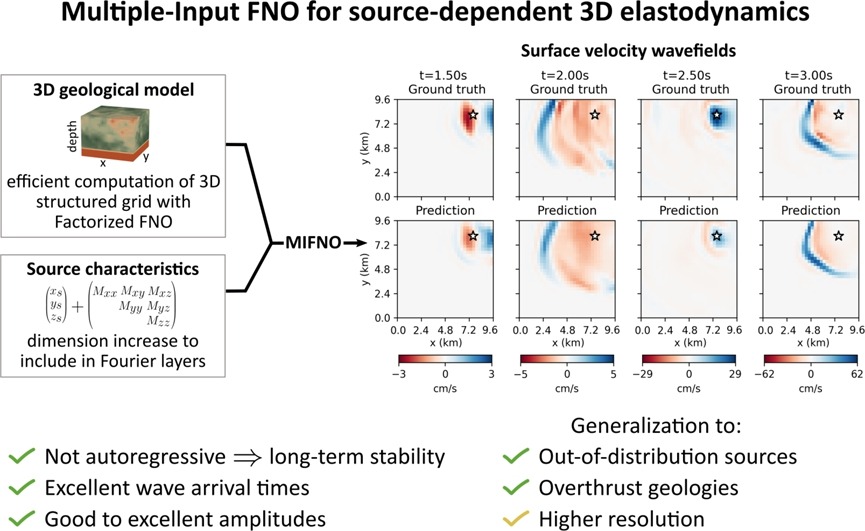   Multiple-Input Fourier Neural Operator (MIFNO) for Source-Dependent 3D Elastodynamics

   Fanny Lehmann, Filippo Gatti, and Didier Clouteau

   Journal of Computational Physics, Apr 2025

   Abs DOI

   Numerical simulations are essential tools to evaluate the solution of the wave equation in complex settings, such as three-dimensional (3D) domains with heterogeneous properties. However, their application is limited by high computational costs and existing surrogate models lack the flexibility of numerical solvers. This work introduces the Multiple-Input Fourier Neural Operator (MIFNO) to deal with structured 3D fields representing material properties as well as vectors describing the source characteristics. The MIFNO is applied to the problem of elastic wave propagation in the Earth’s crust. It is trained on the HEMEWS-3D database containing Image 1 earthquake simulations in different heterogeneous domains with random source positions and orientations. Outputs are time- and space-dependent surface wavefields. The MIFNO predictions are assessed as good to excellent based on Goodness-Of-Fit (GOF) criteria. Wave arrival times and wave fronts propagation are very accurate since Image 2 of the predictions have an excellent phase GOF (larger than Image 3). The fluctuations amplitudes are good for Image 4 of the predictions (envelope GOF larger than Image 5) and excellent for Image 6. The envelope score is hindered by the small-scale fluctuations that are challenging to capture due to the spectral bias inherent to neural networks and the complex physical phenomena associated with high-frequency features. Nevertheless, the MIFNO can generalize to sources located outside the training domain and it shows good generalization ability to a real complex overthrust geology. When focusing on a region of interest, transfer learning is an efficient approach to improve the accuracy with limited additional costs, since GOF scores improved by more than 1 GOF unit with only Image 7 additional specific samples. The MIFNO is the first surrogate model offering the flexibility of an earthquake simulator with varying sources and material properties. Its good accuracy and massive speed-up offer new perspectives to replace numerical simulations in many-query problems.

3. 

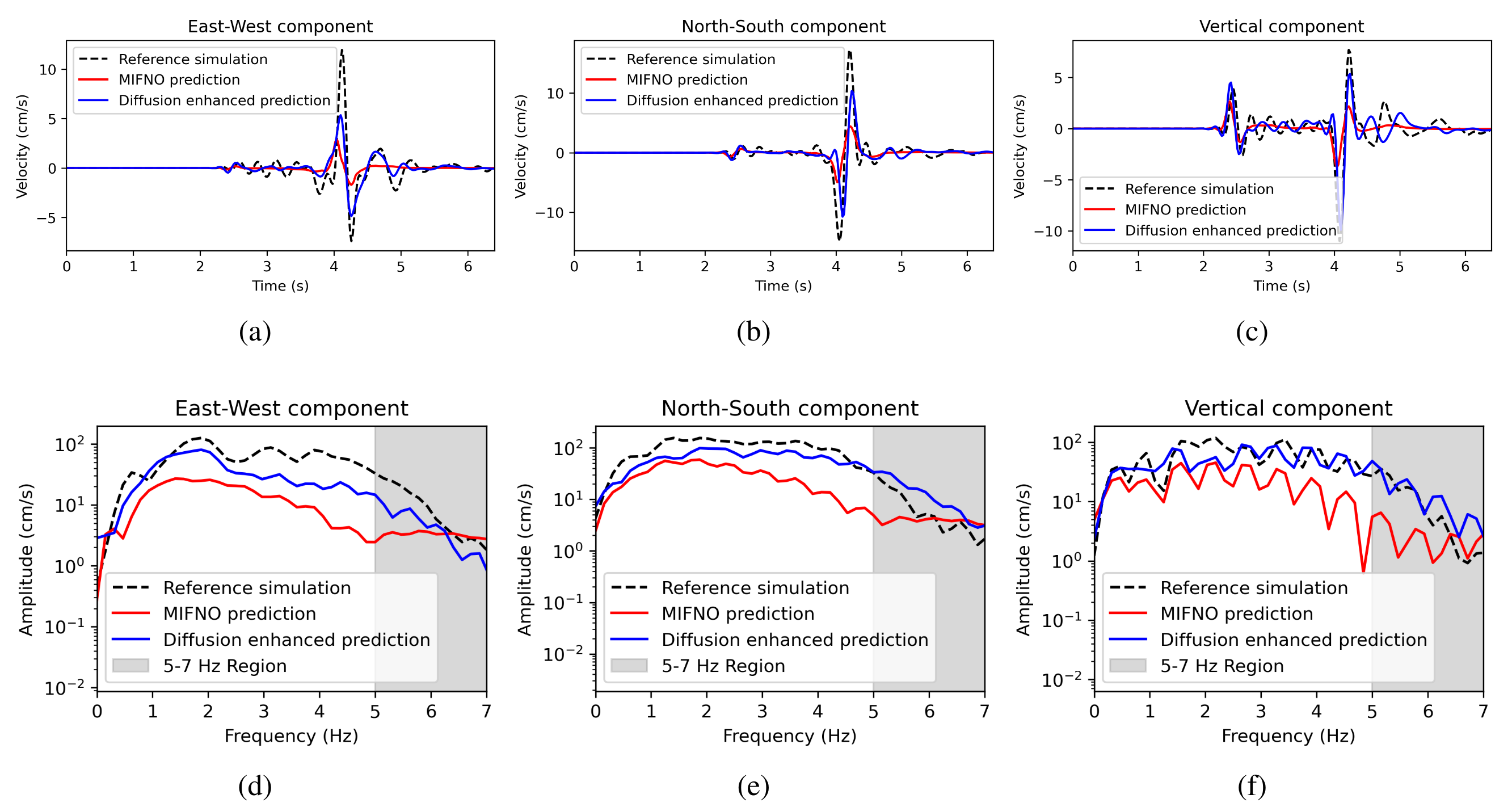   Integrating Fourier Neural Operators with Diffusion Models to Improve Spectral Representation of Synthetic Earthquake Ground Motion Response

   Niccolò Perrone, Fanny Lehmann, Hugo Gabrielidis, Stefania Fresca, and Filippo Gatti

   Apr 2025

   Abs DOI

   Nuclear reactor buildings must be designed to withstand the dynamic load induced by strong ground motion earthquakes. For this reason, their structural behavior must be assessed in multiple realistic ground shaking scenarios (e.g., the Maximum Credible Earthquake). However, earthquake catalogs and recorded seismograms may not always be available in the region of interest. Therefore, synthetic earthquake ground motion is progressively being employed, although with some due precautions: earthquake physics is sometimes not well enough understood to be accurately reproduced with numerical tools, and the underlying epistemic uncertainties lead to prohibitive computational costs related to model calibration. In this study, we propose an AI physics-based approach to generate synthetic ground motion, based on the combination of a neural operator that approximates the elastodynamics Green’s operator in arbitrary source-geology setups, enhanced by a denoising diffusion probabilistic model. The diffusion model is trained to correct the ground motion time series generated by the neural operator. Our results show that such an approach promisingly enhances the realism of the generated synthetic seismograms, with frequency biases and Goodness-Of-Fit (GOF) scores being improved by the diffusion model. This indicates that the latter is capable to mitigate the mid-frequency spectral falloff observed in the time series generated by the neural operator. Our method showcases fast and cheap inference in different site and source conditions.

2024

1. 

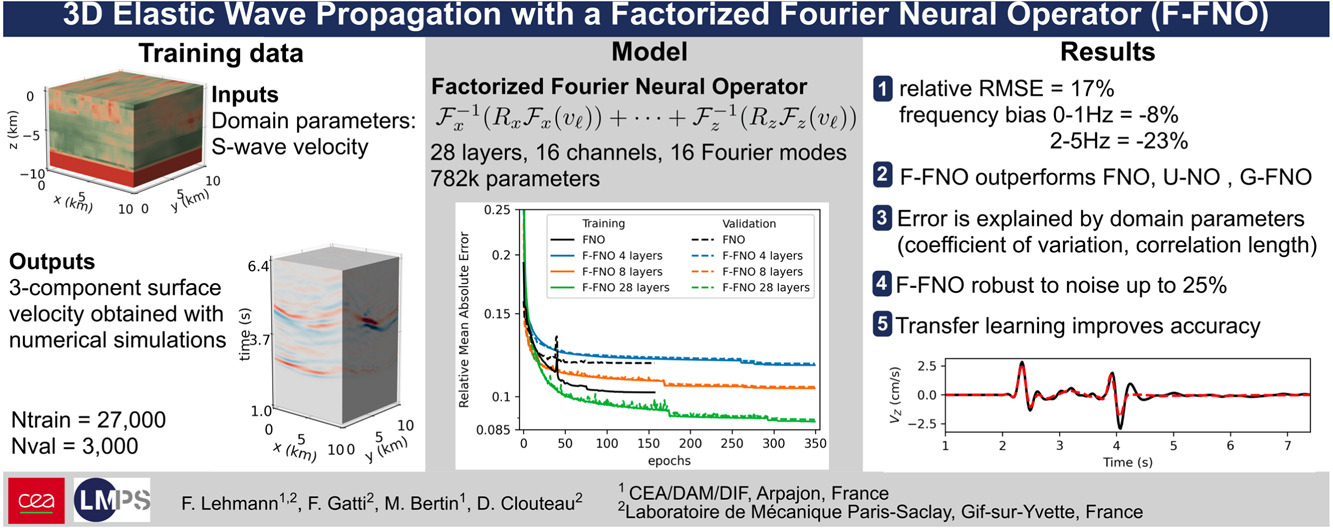   3D Elastic Wave Propagation with a Factorized Fourier Neural Operator (F-FNO)

   Fanny Lehmann, Filippo Gatti, Michaël Bertin, and Didier Clouteau

   Computer Methods in Applied Mechanics and Engineering, Feb 2024

   Abs DOI

   Numerical simulations are computationally demanding in three-dimensional (3D) settings but they are often required to accurately represent physical phenomena. Neural operators have emerged as powerful surrogate models to alleviate the computational costs of simulations. However, neural operators applications in 3D remain sparse, mainly due to the difficulty of obtaining training databases for supervised learning and the size of 3D neural operators that poses memory challenges. This work focuses on the propagation of elastic waves in 3D domains and showcases the Factorized Fourier Neural Operator (F-FNO) as an efficient and accurate surrogate model. The F-FNO is trained on the publicly available HEMEW-3D database of 30\hphantom,000 wavefields simulations in realistic heterogeneous domains. The F-FNO predicts space- and time-dependent (3D) surface wavefields depending on the characteristics of the propagation domain (characterized by the velocity of shear waves). Four FNO variants are compared and extensive investigations on the influence of hyperparameters and training strategies are conducted. The two most influential hyperparameters are the number of layers and the number of channels, meaning that richer models are more accurate. On the contrary, increasing the number of Fourier modes had little influence and did not reduce the spectral bias that causes an underestimation of high-frequency patterns. The F-FNO is sensitive to heterogeneities in the inputs but robust to the addition of noise. Additionally, it possesses good generalization ability to out-of-distribution data and transfer learning is very beneficial to improve the predictions in tailored applications.

2. Physics-Based Simulations of 3D Wave Propagation - Case Study Deriving from the Le Teil Earthquake

   Fanny Lehmann

   Jun 2024

   Abs DOI

   This dataset contains 4,000 simulation results of the 3D elastic wave equation in a setting deriving from the Le Teil earthquake (France, 2019). The elastic wave equation governs the propagation of waves in a 3D propagation medium. Two types of data are given in this dataset: a materials dataset and a velocity dataset. Materials dataset Each material describes the propagation domain used for one numerical simulation. It is built from non-stationary random fields added to the reference 1D velocity profile and corresponds to the velocity of shear waves. The minimum value is 1500m/s and the maximum is 4500m/s. All materials contain a 1800m-thick bottom layer with a constant velocity of 4500m/s.  All materials are 3D arrays of shape 32 x 32 x 32.They correspond to a physical size of 9.6 x 9.6 x 9.6km^3.  Practical use Materials are provided as ‘.npy‘ arrays, readable with python: ‘a = np.load(‘materials0-1999.npy’)‘Each file contains 2000 materials. Therefore, ‘a‘ is of shape (2000, 32, 32, 32). Indices correspond to the material index, the x coordinate (from West to East), the y coordinate (from South to North), and the z coordinate (from bottom to top).  Velocity dataset The velocity dataset contains the velocity wavefields simulated at the surface of each propagation domain. They have been generated by solving the 3D elastic wave equation with the high-performance computing code SEM3D based on the Spectral Element Method (https://github.com/sem3d/SEM). To each material described above corresponds one velocity field, obtained by the propagation of waves through this material. Velocity fields were recorded by a grid of 16 x 16 virtual sensors located at the surface of the propagation domain between 150m and 450m (600m between consecutive sensors). Each sensor records the 3-component velocity with a 100Hz sampling between 0s and 20s.  Computational details: The computational mesh was designed with elements of size 300m and 7 Gauss-Lobato-Legendre quadrature points. It can accurately represent the propagation of waves up to 5Hz frequency. Waves were generated by a point-wise source placed at the bottom of the domain, inside the constant layer (the position of the source is 4800, 4800, -8400m). The seismic source derives from the Le Teil earthquake [Delouis et al., 2021, doi:10.5802/crgeos.78]. The seismic source is described by a moment tensor with fixed orientation (strike = 48°, dip = 45°, and rake = 88°) and amplitude (moment magnitude M0=2.47 ⋅ 10^16 N.m). Practical use Results are given in .feather dataframes, readable with pandas library in Python: v = pd.read_feather(‘velocity0-99.feather’). Each dataframe contains 100 simulation results. Each row of the dataframe has the following format:  run field x y z 0.0 0.01 0.02 ... 19.98 19.99 12 Veloc E 150.0 770.0 -1.0 0 0 0 ... 1.1e-5 1.0e-5 12 Veloc N 150.0 770.0 -1.0 0 0 0 ... 3e-6 3e-6 12 Veloc Z 150.0 770.0 -1.0 0 0 0 ... -2.6e-5 -2.7e-5 ... ... ... ... ... ... ... ... ... ... ... where ‘run‘ indicates the index of the material used in this simulation, ‘field‘ indicates the component of the velocity field (‘Veloc E‘ for East-West, ‘Veloc N‘ for North-South, ‘Veloc Z‘ for Vertical). ‘x‘, ‘y‘, ‘z‘ are the coordinates of the sensor (in meters). The next 2000 columns contain the velocity field for times 0, 0.01, …, 19.99. Related work This dataset was used to fine-tune a Factorized Fourier Neural Operator (F-FNO, Lehmann et al. 2024, doi:10.1016/j.cma.2023.116718) to predict ground motion wavefields from 3D geologies. The code to train the F-FNO is available at https://github.com/lehmannfa/HEMEW3D

3. 

   A Surrogate Model of Elastic Wave Propagation to Quantify Uncertainties in Seismic Hazard Analysis

   Fanny Lehmann

   Jun 2024

   Abs URL

   The propagation of seismic waves in the ground is subject to many sources of uncertainties, ranging from the uncertain activity of geological faults to the incomplete knowledge of mechanical properties inside the Earth’s crust. To properly assess seismic hazard, it then becomes essential to quantify how uncertainties influence the intensity of ground motion generated by earthquakes.In areas with low-to-moderate seismicity, like most regions in metropolitan France, seismic records are too sparse to evaluate ground motion uncertainties. In this situation, numerical simulations are the only option to estimate ground motion intensity, but their high computational costs prevent most uncertainty analyses. In this thesis, we design a surrogate model that can replace the numerical solver by drastically reducing the computational costs while preserving its flexibility and a satisfying accuracy.We first illustrate the influence of geological heterogeneities on ground motion intensity in the context of the Mw4.9 Le Teil earthquake (Ardèche, France, 2019). Heterogeneities are added to a regional geological model in the form of random fields, and we show that it generates more realistic ground motion. However, heterogeneities also lead to a large variability between samples.To study this variability systematically, we build a database of 30,000 heterogeneous 3D geological models, and inside each geology, seismic waves are propagated from a random source using the spectral element code SEM3D. The database is then used to train a surrogate model in a purely data-driven framework.To design the surrogate model, we propose an extension of the Fourier Neural Operator called the Multiple Input Fourier Neural Operator (MIFNO). The MIFNO takes as inputs a 3D geology and a vector of source parameters to predict 3D ground motion. Ground motion is a time-dependent surface wavefield, but we do not need any time iteration thanks to a depth-to-time conversion. We characterize the MIFNO prediction error and explore the MIFNO generalization ability to out-of-distribution data.We finally take advantage of transfer learning to further improve the MIFNO accuracy in the context of the Le Teil earthquake. With this fine-tuned surrogate model, we obtain statistical distributions of several quantities of interest in seismic hazard assessment. They are coherent with numerical simulations and provide confidence intervals that were out of reach with existing methods.

4. 

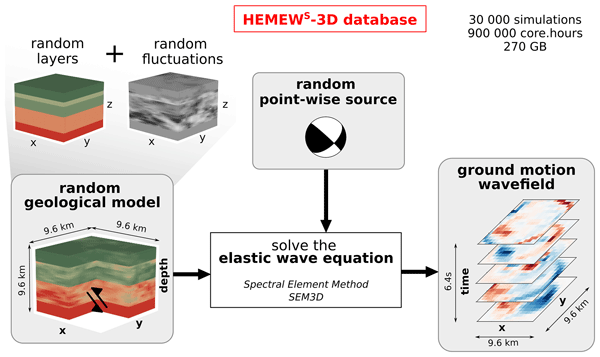   Synthetic Ground Motions in Heterogeneous Geologies from Various Sources: The HEMEW^S-3D Database

   Fanny Lehmann, Filippo Gatti, Michaël Bertin, and Didier Clouteau

   Earth System Science Data, Jun 2024

   Abs DOI

   The ever-improving performances of physics-based simulations and the rapid developments of deep learning are offering new perspectives to study earthquake-induced ground motion. Due to the large amount of data required to train deep neural networks, applications have so far been limited to recorded data or two-dimensional (2D) simulations. To bridge the gap between deep learning and high-fidelity numerical simulations, this work introduces a new database of physics-based earthquake simulations. The HEterogeneous Materials and Elastic Waves with Source variability in 3D (HEMEWS-3D) database comprises 30,000 simulations of elastic wave propagation in 3D geological domains. Each domain is parametrized by a different geological model built from a random arrangement of layers augmented by random fields that represent heterogeneities. Elastic waves originate from a randomly located pointwise source parametrized by a random moment tensor. For each simulation, ground motion is synthesized at the surface by a grid of virtual sensors. The high frequency of waveforms (f_max = 5Hz) allows for extensive analyses of surface ground motion. Existing and foreseen applications range from statistical analyses of the ground motion variability and machine learning methods on geological models to deep-learning-based predictions of ground motion that depend on 3D heterogeneous geologies and source properties. Data are available at https://doi.org/10.57745/LAI6YU (Lehmann, 2023).

5. 

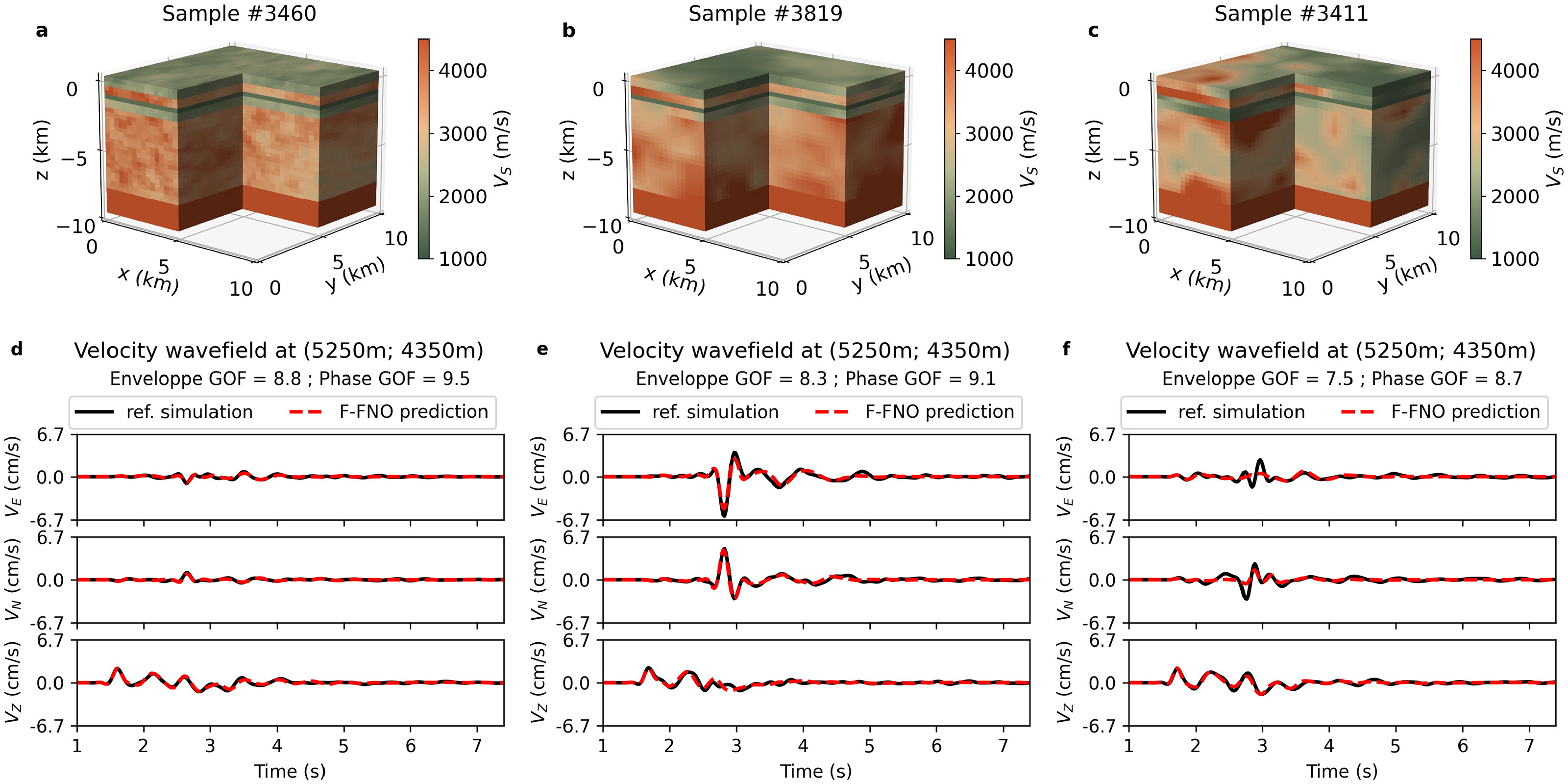   Uncertainty Propagation from Crustal Geologies to Rock-Site Ground Motion with a Fourier Neural Operator

   Fanny Lehmann, Filippo Gatti, Michaël Bertin, Damien Grenié, and Didier Clouteau

   European Journal of Environmental and Civil Engineering, Jun 2024

   Abs DOI

   Seismic hazard analyses in the area of a nuclear installation must account for a large number of uncertainties, including limited geological knowledge. Combining the accuracy of physics-based simulations with the expressivity of deep neural networks can help to quantify the influence of crustal geological uncertainties on surface ground motion. This work uses a Factorised Fourier Neural Operator (F-FNO) to learn the relationship between 3D crustal heterogeneous geologies and time-dependent wavefields at the Earth’s surface up to a 5Hz maximal frequency. The F-FNO is pretrained on a generic database and then, fine-tuned with only 250 samples targeted to the Le Teil region (South-Eastern France). The F-FNO correctly predicts the wave arrival times and the main wavefronts. As quantified by Goodness-Of-Fit (GOF) criteria, 83% of predictions have excellent phase GOF and 75% have very good envelope GOF. The Peak Ground Velocity and Pseudo-Spectral Acceleration are also accurate, especially for geologies with low-to-moderate heterogeneities. Thanks to the F-FNO speed, ground motion distributions can be easily computed and provide safety margins compared to 1D simulations. These results show that the F-FNO is an efficient surrogate model to quantify the range of ground motion a nuclear installation could face in the presence of geological uncertainties.

2023

1. Fourier Neural Operator Surrogate Model to Predict 3D Seismic Waves Propagation

   Fanny Lehmann, Filippo Gatti, Michaël Bertin, and Didier Clouteau

   In 5th ECCOMAS Thematic Conference on Uncertainty Quantification in Computational Sciences and Engineering, Jun 2023

   Abs DOI

   With the recent rise of neural operators, scientific machine learning offers new solutions to quantify uncertainties associated with high-fidelity numerical simulations. Traditional neural networks, such as Convolutional Neural Networks (CNN) or Physics-Informed Neural Networks (PINN), are restricted to the prediction of solutions in a predefined configuration. With neural operators, one can learn the general solution of Partial Differential Equations, such as the elastic wave equation, with varying parameters. There have been very few applications of neural operators in seismology. All of them were limited to two-dimensional settings, although the importance of three-dimensional (3D) effects is well known.

2. Physics-Based Simulations of 3D Wave Propagation: A Dataset for Scientific Machine Learning

   Fanny Lehmann

   Aug 2023

   DOI
3. Seismic Hazard Analysis with a Factorized Fourier Neural Operator (F-FNO) Surrogate Model Enhanced by Transfer Learning

   Fanny Lehmann, Filippo Gatti, Michaël Bertin, and Didier Clouteau

   In NeurIPS 2023 AI for Science Workshop, Aug 2023

   Abs URL

   Seismic hazard analyses in the area of a nuclear installation must account for a large number of uncertainties, including limited geological knowledge. It is known that some geological features can create site-effects that considerably amplify ground motion. Combining the accuracy of physics-based simulations with the expressivity of deep neural networks can help quantifying the influence of geological heterogeneities on surface ground motion. This work demonstrates the use of a Factorized Fourier Neural Operator (F-FNO) that learns the relationship between 3D heterogeneous geologies and time-dependent surface wavefields. The F-FNO was pretrained on the generic HEMEW-3D database made of 30 000 samples. Then, a smaller database was built specifically for the region of the Le Teil earthquake (South-Eastern France) and the F-FNO was further trained with only 250 specific samples. Transfer learning improved the prediction error by 22 %. As quantified by the Goodness-Of-Fit (GOF) criteria, 90 % of predictions had excellent phase GOF (62 % for the enveloppe GOF). Although the intensity measures of surface ground motion were, in average, slightly underestimated by the FNO, considering a set of heterogeneous geologies always led to ground motion intensities larger than those obtained from a single homogeneous geology. These results suggest that neural operators are an efficient tool to quantify the range of ground motions that a nuclear installation could face in the presence of geological uncertainties. The HEMEW-3D database and the pretrained F-FNO model are publicly available to facilitate further developments and applications.

2022

1. 3D S-wave Velocity Profiles with Random Fields

   Fanny Lehmann

   Dec 2022

   Abs DOI

   This dataset contains 100,000 3D matrices representing S-wave velocity profiles with random fields. The spatial resolution corresponds to a grid of 9.6 x 9.6 x 9.6km with a spatial step of 300m (matrices are of size 33 x 33 x 33). Velocities go from 1,071 to 4,500m/s. Each profile contains a 1.8km-thick bottom layer at constant velocity 4500m/s. Above, the profile contains between 1 and 6 layers of random thickness. In each layer, the mean velocity is chosen uniformly in [1,785; 3,214m/s] and the coefficient of variation follows a Gaussian distribution N(0.2; 0.1). Then, a correlation length is chosen randomly among 1.5, 3, 4.5, 6 km in all three directions for each layer. The random fields’ kernel has a von Karman correlation with a Hurst exponent of 0.1 and log-normal marginal distributions.

2. 

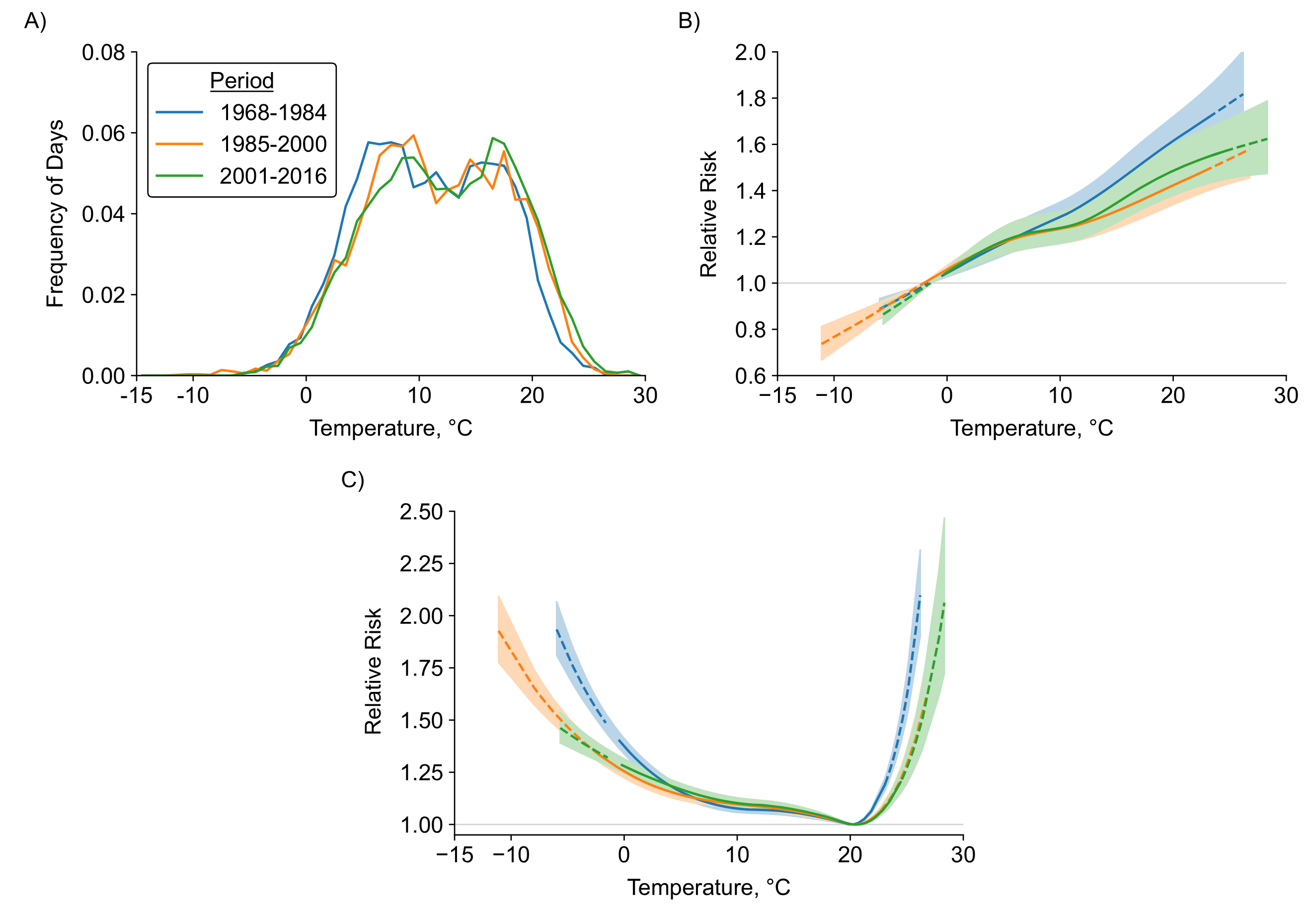   Association of Daily Temperature With Suicide Mortality: A Comparison With Other Causes of Death and Characterization of Possible Attenuation Across 5 Decades

   Fanny Lehmann, Pierre-Etienne Alary, Grégoire Rey, and Rémy Slama

   American Journal of Epidemiology, Nov 2022

   Abs DOI

   Suicide is one of the leading causes of death in young adults in many Western countries. We examined the short-term association of temperature with cause-specific mortality, comparing suicide with other causes of death and describing possible attenuation of associations with temperature across decades. We considered all deaths that occurred in France between 1968 and 2016. For each cause of death, we conducted a 2-stage meta-analysis of associations with daily temperature. We stratified the association across time periods. A total of 502,017 deaths by suicide were recorded over 49 years. Temperature was monotonically associated with suicide mortality. The strongest association was found at lag 0 days. The relative risk of suicide mortality at the 99th (compared with the 1st) temperature percentile was 1.54 (95% confidence interval, 1.46, 1.63). Among all causes of death, suicide was the only cause displaying a monotonic trend with temperature and ranked seventh for heat-related mortality; 2 other causes of death implying the nervous system ranked third and fourth. Associations with temperature attenuated between the 1968–1984 and 1985–2000 periods for all-cause mortality and suicide mortality, without clear further attenuation in the 2001–2016 period. The robust short-term monotonic association between temperature and suicide risk could be considered in heat effects– and suicide-related prevention campaigns.

3. Compilation of Hydrological Datasets at the Global Scale

   Fanny Lehmann

   Aug 2022

   Abs DOI

   Hydrological variables (evapotranspiration, precipitation, runoff, and terrestrial water storage) are distributed through several datasets that do not have the same characteristics (spatial and temporal coverage, spatial and temporal resolution). This dataset aims at providing a coherent gathering of all datasets available as of January 2021, covering at least the period from 2003 to 2014, and from 50°S to 50°N. This file contains: 14 datasets for evapotranspiration (ERA5-Land, FLUXCOM, GLDAS2.2 CLSM2.5, GLDAS2.1 CLSM2.5, GLDAS2.1 NOAH3.6, GLDAS VIC4.1.2, GLDAS2.0 CLSM2.5, GLDAS2.0 NOAH3.6, GLDAS2.0 VIC4.1.2, GLEAM, JRA55, MERRA2, MOD16, and SEBBop) 11 datasets for precipitation (CPC, CRU, ERA5-Land, PGF, GPCC, GPCP, GPM, JRA55, MERRA2, MSWEP, and TRMM) 11 datasets for runoff (ERA5-Land, GLDAS2.2 CLSM2.5, GLDAS2.1 CLSM2.5, GLDAS2.1 NOAH3.6, GLDAS VIC4.1.2, GLDAS2.0 CLSM2.5, GLDAS2.0 NOAH3.6, GLDAS2.0 VIC4.1.2, GRUN, JRA55, and MERRA2) 2 datasets for terrestrial water storage (GRACE CSR mascons, and GRACE JPL mascons) Each dataset is given as the original version (on a regular grid) and also as a post-treated file averaged for 189 river basins (whose borders are also provided).

4. 

   How Well Are We Able to Close the Water Budget at the Global Scale?

   Fanny Lehmann, Bramha Dutt Vishwakarma, and Jonathan Bamber

   Hydrology and Earth System Sciences, Jan 2022

   Abs DOI

   The water budget equation describes the exchange of water between the land, ocean, and atmosphere. Being able to adequately close the water budget gives confidence in our ability to model and/or observe the spatio-temporal variations in the water cycle and its components. Due to advances in observation techniques, satellite sensors, and modelling, a number of data products are available that represent the components of water budget in both space and time. Despite these advances, closure of the water budget at the global scale has been elusive. In this study, we attempt to close the global water budget using precipitation, evapotranspiration, and runoff data at the catchment scale. The large number of recent state-of-the-art datasets provides a new evaluation of well-used datasets. These estimates are compared to terrestrial water storage (TWS) changes as measured by the Gravity Recovery And Climate Experiment (GRACE) satellite mission. We investigated 189 river basins covering more than 90% of the continental land area. TWS changes derived from the water balance equation were compared against GRACE data using two metrics: the Nash–Sutcliffe efficiency (NSE) and the cyclostationary NSE. These metrics were used to assess the performance of more than 1600 combinations of the various datasets considered. We found a positive NSE and cyclostationary NSE in 99% and 62% of the basins examined respectively. This means that TWS changes reconstructed from the water balance equation were more accurate than the long-term (NSE) and monthly (cyclostationary NSE) mean of GRACE time series in the corresponding basins. By analysing different combinations of the datasets that make up the water balance, we identified data products that performed well in certain regions based on, for example, climatic zone. We identified that some of the good results were obtained due to the cancellation of errors in poor estimates of water budget components. Therefore, we used coefficients of variation to determine the relative quality of a data product, which helped us to identify bad combinations giving us good results. In general, water budget components from ERA5-Land and the Catchment Land Surface Model (CLSM) performed better than other products for most climatic zones. Conversely, the latest version of CLSM, v2.2, performed poorly for evapotranspiration in snow-dominated catchments compared, for example, with its predecessor and other datasets available. Thus, the nature of the catchment dynamics and balance between components affects the optimum combination of datasets. For regional studies, the combination of datasets that provides the most realistic TWS for a basin will depend on its climatic conditions and factors that cannot be determined a priori. We believe that the results of this study provide a road map for studying the water budget at catchment scale.

5. 

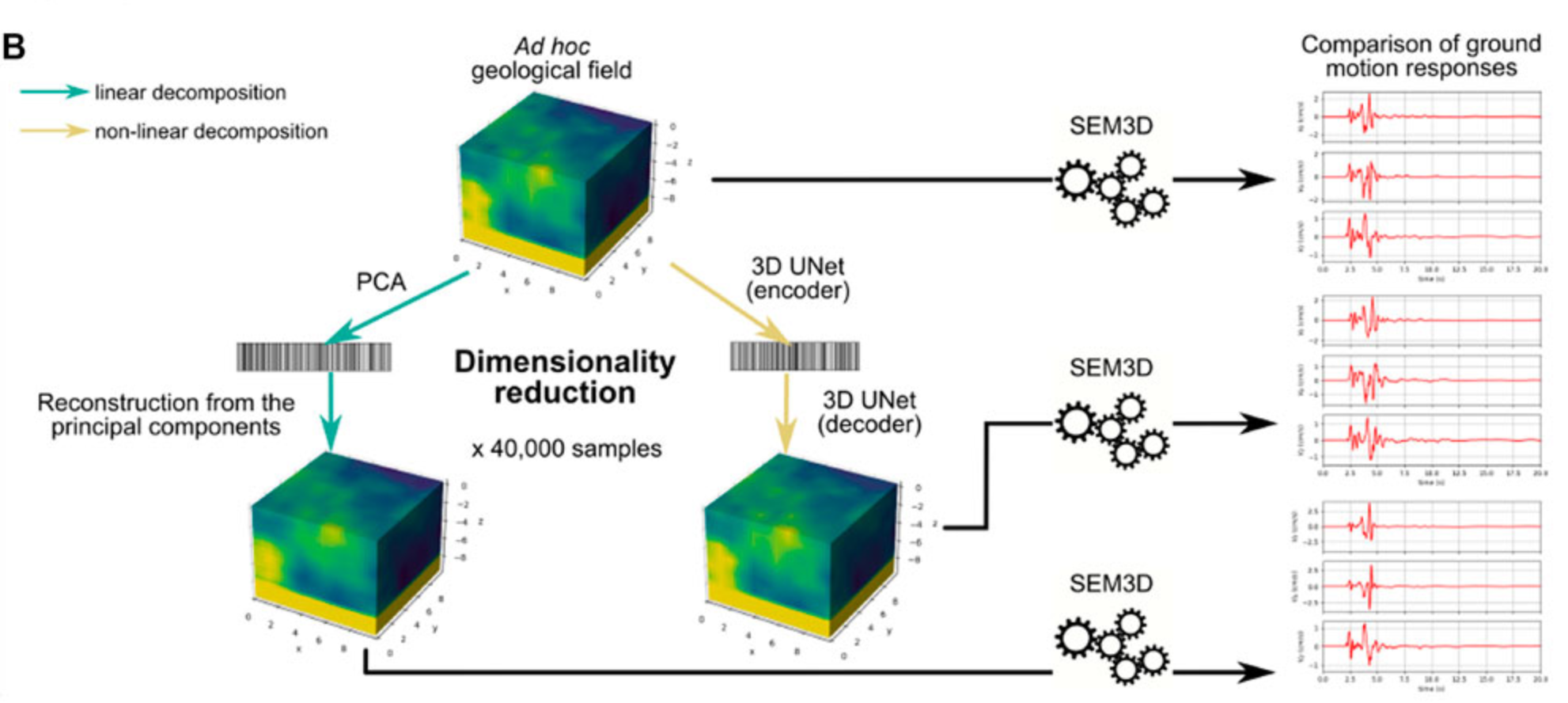   Machine Learning Opportunities to Conduct High-Fidelity Earthquake Simulations in Multi-Scale Heterogeneous Geology

   Fanny Lehmann, Filippo Gatti, Michaël Bertin, and Didier Clouteau

   Frontiers in Earth Science, Jan 2022

   Abs DOI

   The 2019 Le Teil earthquake is an illustrative example of a moderate (M\textexclamdownsub\textquestiondownW\textexclamdown/sub\textquestiondown 4.9) yet damaging event, occurring at shallow depth (≈1 km) in a region with little to no geophysical data available. Therefore, using a high-fidelity wave propagation code, we performed numerical simulations of the Le Teil earthquake in a highly uncertain framework, investigating several seismic sources and geological set-ups. With respect to the former aspect, a point-source model and an extended kinematic fault model were compared. The latter aspect was investigated by comparing a 1D-layered to a 3D geological model. Those models were enhanced with random fluctuations, in order to obtain three alternative non-stationary random geological fields. The synthetic waveforms obtained from regional geophysical models were globally coherent with the recorded ones. The extended fault source model seemed more realistic than the point-source model. In addition, some geological random fields improved the synthetics’ agreement with the recordings. However, the three random field samplings led to a high variability in induced ground motion responses. Given the computational burden of high-fidelity simulations, we used two dimensionality reduction methods, namely the Principal Component Analysis (PCA) and a deep neural network (3D UNet), to investigate this variability. The methods were applied to a database of 40,000 3D geological random fields. Both the PCA and the 3D UNet condensed the variability of the 3D geological fields into a few components. These were sufficient to reconstruct the original fields with great accuracy. More importantly, the seismic response arising from the propagation throughout the reconstructed fields was in excellent agreement with the response of the original geological fields in more than 75% of the dataset. By building a structured ensemble of complex geological fields from their reduced representation, it may become possible to find a relationship between the reduced representation and the generated ground motion. Thus, our study proves the interest of dimensionality reduction to perform uncertainty analyses in complex geological media.

2021

1. 

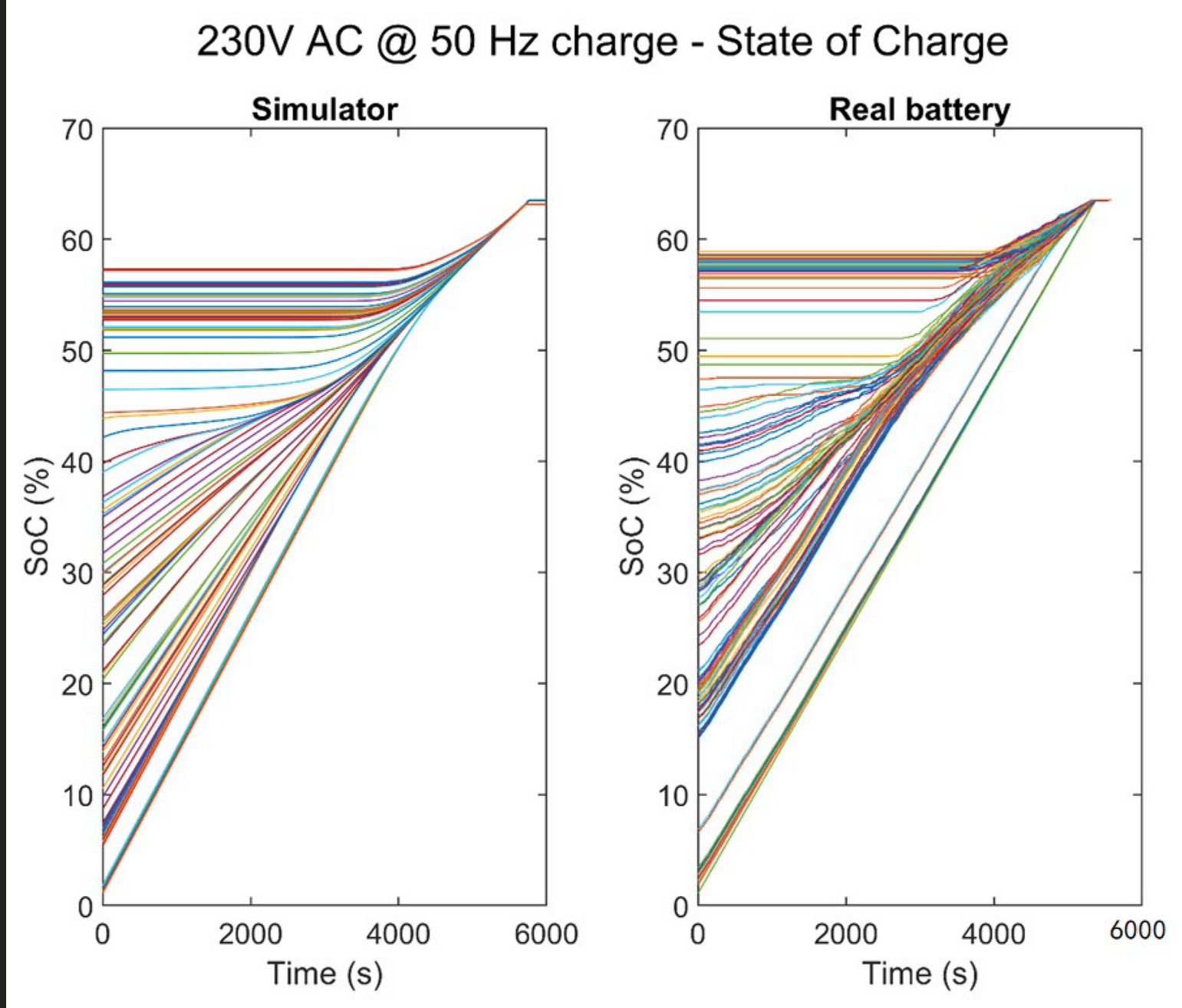   Performance Analysis of a Novel High Frequency Self-Reconfigurable Battery

   Rémy Thomas, Fanny Lehmann, Jérôme Blatter, Ghislain Despesse, and Vincent Heiries

   World Electric Vehicle Journal, Jan 2021

   Abs DOI

   Self-reconfigurable battery architectures have gained a lot of interest recently in the literature, with more and more advanced functionalities. This paper describes the performance analysis of our proposed High Frequency Self-Reconfigurable Battery (HF SRB). To evaluate specific features with long-term dependencies of our system, a full functional behavioral simulator was developed. A comparison with a real 128-level HF SRB validated the simulator operation. The balancing performances obtained on vehicle test cycles showed the cell capacity discrepancy that the HF SRB is capable of handling in a single complete charge or discharge cycle. The magnitude of this gap demonstrated the extent to which the HF SRB is capable of operating with second life cells or even different chemistry mixes.